Does this sound familiar? Your child successfully completes their long division problems during homework time, but the very next day, it's as if they've never seen division before. As a dyscalculia specialist, I hear this from parents all the time. I've found that a proven approach, initially introduced by American Psychologist Jerome Bruner and called concrete-representational-abstract (CRA), can make a remarkable difference in helping students build lasting understanding.

The secret lies in a three-step journey: concrete, representational, and then abstract. Let me show you how this works with multiplication facts, something many students with dyscalculia struggle to master. First, we use integer blocks to build an area model of the fact - something your child can touch and manipulate. Once they're comfortable with the blocks, we move to the crucial bridge step: having them recreate what they built by drawing an area model on graph paper or freehand. They learn to skip count row by row to find the product, connecting the physical model to their drawing. Finally, they write out the complete fact with its factors and product.

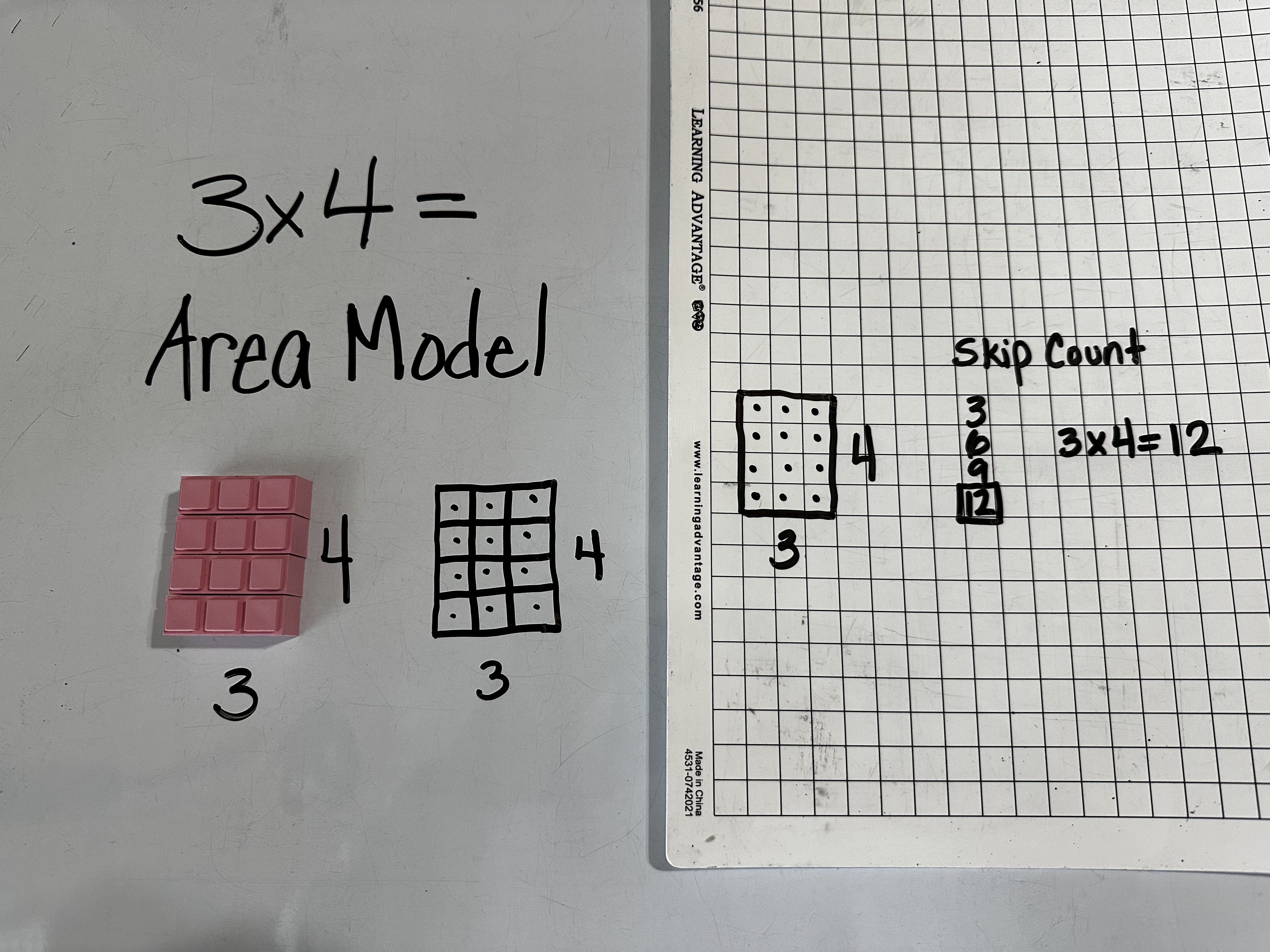
 I know what some of you might be thinking - working with manipulatives feels messy and time-consuming. You might be tempted to just show your child how you learned math. But here's the thing: your child's brain processes math differently, and traditional methods often don't make sense to them. The good news? None of these supporting stages are forever. Think of them as scaffolding - necessary while building understanding, but temporary. Your child will naturally progress from using blocks to drawing their math, and finally to working with just numbers as their understanding grows stronger.

And yes, when a new math concept comes along, your child might need to start back with the blocks again - that's completely normal! Each time they go through this progression, they're building not just math skills, but confidence in their ability to learn new concepts.

Making Daily Practice Work

Understanding the Flow Between Stages

Your child will often work at multiple stages simultaneously - and that's exactly how it should be! They might use blocks for some problems while drawing others, gradually building toward abstract solutions. When they can clearly explain what the blocks represent and accurately draw the same concept, they're typically ready to rely less on the physical materials. Try reducing the number of problems that use blocks each day, while keeping them handy just in case.

Handling Tough Days

We all have days when things just don't click - and that's normal! If your child seems to be struggling more than usual, take it as a signal to step back. Reintroducing the blocks or returning to drawing can help refresh their memory. Think of it like a reset button that helps them reconnect with the concept. Often, after working with manipulatives for just a few problems, they'll be ready to return to more abstract work.

Making Practice Flexible

Daily practice works best when it adapts to your child's needs:

- Mix problems that use different approaches (blocks, drawings, numbers)

- Keep manipulatives easily accessible, even for skills that seem mastered

- Allow your child to choose which tool helps them understand best

- Celebrate their ability to recognize when they need more support

Building Independence

The goal isn't to rush through these stages - it's to help your child become confident in recognizing how they learn best. When they understand that moving between concrete, representational, and abstract work is normal and helpful, they develop valuable self-advocacy skills.

Signs of Success

The most powerful sign of progress isn't necessarily when your child can solve every problem abstractly - it's when they can recognize what they need to understand and solve it. If your child reaches for paper to sketch out a challenging problem instead of freezing or giving up, that's a huge win! This self-awareness and problem-solving independence is actually more valuable than memorizing procedures.

Remember: drawing or sketching math problems is a legitimate problem-solving strategy at any age. Many successful adults sketch out complex problems to better understand them. When your child can independently recognize they need to draw something out and then successfully use that drawing to find the solution, they're demonstrating real mathematical thinking.

Making Daily Practice Sustainable

Keep it Low-Pressure

- Have scratch paper always available for drawings

- Normalize the idea that different problems might need different approaches

- Celebrate when your child independently chooses to draw out a problem

Build on Success

- Notice and point out when drawing helps solve a tricky problem

- Help your child see that using representational strategies isn't a step backward - it's a powerful problem-solving tool

- Encourage them to teach you their drawing strategies - explaining helps cement their understanding

Support Independence

- Make drawing materials easily accessible during homework time

- Let your child develop their own ways of representing different types of problems

- Trust that with consistent practice, they'll find the approaches that work best for them

A Note to Parents and Teachers

When a student has dyscalculia, multi-sensory experiences aren't just helpful - they're often essential for processing mathematical concepts. Think of drawing or sketching math problems as your child's way of creating their own multi-sensory learning experience. When they take the initiative to represent a problem visually, they're not avoiding 'real' math - they're showing you their mathematical thinking in action.

In fact, these drawings are a powerful form of 'showing their work.' While traditional math education often expects students to show their work through number sentences and algorithms alone, a detailed drawing can reveal even more about a student's problem-solving process and understanding. It demonstrates:

- Their ability to visualize mathematical relationships

- Their understanding of the problem structure

- Their initiative in finding effective learning strategies

- Their development of independence in math thinking

Supporting Your Child's Success

Remember that daily practice isn't about pushing toward abstract calculation as quickly as possible. It's about:

- Encouraging your child to use tools that help them truly understand

- Celebrating when they independently create visual supports

- Recognizing that their need for multi-sensory math experiences is part of how their brain processes mathematical information

- Supporting their development of sustainable, effective problem-solving strategies

When we embrace these drawing and representational strategies as valuable mathematical tools rather than temporary supports, we empower students with dyscalculia to become confident, independent mathematical thinkers.

Subscribe below for a free download where you will discover how math games can be used as a part of your student's multi-sensory math experience.